
There is no model of the theory of gravitation today, other than the mathematical form.
It this were the only law of this character it would be interesting and rather annoying. But what turns out to be true is that the more we investigate, the more laws we find, and the deeper we penetrate nature, the more this disease persists. Every one of our laws is a purely mathematical statement in rather complex and abstruse mathematics. Newton’s statement of the law of gravitation is relatively simple mathematics. It gets more and more abstruse and more and more difficult as we go on. Why? I have not the slightest idea. It is only my purpose here to tell you about this fact. The burden of the lecture is just to emphasize the fact that it is impossible to explain honestly the beauties of the laws of nature in a way that people can feel, without their having some deep understanding of mathematics. I am sorry, but this seems to be the case.
You might say, “All right, then if there is no explanation of the law, at least tell me what the law is. Why not tell me in words instead of symbols? Mathematics is just a language, and I want to be able to translate the language.” In fact I can, with patience, and I think I partly did. I could go a little further and explain in more detail that the equation means that if the distance is twice as far the force is one fourth as much, and so on. I could convert all the symbols into words. In other words I could be kind to the layman as they all sit hopefully waiting for me to explain something. Different people get different reputations for their skill at explaining to the layman in layman’s language these difficult and abstruse subjects. The layman then searches for book after book in the hope that he will avoid the complexities which eventually set in, even with the best expositor of this type. He finds as he reads a generally increasing confusion, one complicated statement after another, one difficult-to-understand thing after another, all apparently disconnected from one another. It becomes obscure, and he hopes that maybe in some other book there is some explanation… The author almost made it- maybe another fellow will make it right.
But I do not think it is possible, because mathematics is not just another language. Mathematics is a language plus reasoning; it is like a language plus logic. Mathematics is a tool for reasoning. It is in fact a big collection of the results of some person’s careful thought and reasoning. By mathematics it is possible to connect one statement to another. For instance, I can say that the force is directed towards the sun. I can also tell you, as I did, that the planet moves so that if I draw a line from the sun to the planet, and draw another line at some definite period, like three weeks, later, then the area that is swung out by the planet is exactly the same as it will be in the next three weeks, and the next three weeks, and so on as it goes around the sun. I can explain both of those statements carefully, but I cannot explain why they are both the same. The apparent enormous complexities of nature, with all its funny laws and rules, each of which has been carefully explained to you, are really very closely interwoven. However, if you do not appreciate the mathematics, you cannot see, among the great variety of facts, that logic permits you to go from one to another.
It may be unbelievable that I can demonstrate that equal areas will be swept out in equal times if the forces are directed towards the sun. So if I may, I will do one demonstration to show you that those two things really are equivalent, so that you can appreciate more than the mere statement of the two laws. I will show that the two laws are connected so that reasoning alone will bring you from one to the other, and that mathematics is just organized reasoning. Then you will appreciate the beauty of the relationship of the statements. I am going to prove the relationship that if the forces are directed towards the sun then equal areas are swept out in equal times.
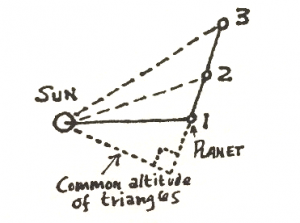
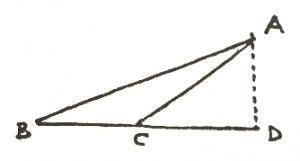
We start with a sun and a planet (Figure 1), and we imagine that at a certain time the planet is at position 1. It is moving in such a way that, say, one second later it has moved to position 2. If the sun did not exert a force on the planet, then, by Galileo’s principle of inertia, it would keep right on going in a straight line. So after the same interval of time, the next second, it would have moved exactly the same distance in the same straight line, to the position 3. First we are going to show that if there is no force, then equal areas are swept out in equal times. I remind you that the area of a triangle is half the base times the altitude, and that the altitude is the vertical distance to the base. If the triangle is obtuse (Figure 2), then the altitude is the vertical height AD and the base is BC.
Now let us compare the areas which would be swept out if the sun exerted no force whatsoever (Figure 1). The two distances 1-2 and 2-3 are equal, remember. The question is, are the two areas equal? Consider the triangle made from the sun and the two points 1 and 2. What is its area? It is the base 1-2, multiplied by half the perpendicular height from the baseline to S. What about the other triangle, the triangle in the motion from 2 to 3? Its area is the base 2-3, times half the perpendicular height to S. The two triangles have the same altitude, and, as I indicated, the same base, and therefore they have the same area. So far so good. If there were no force from the sun, equal areas would be swept out in equal times. But there is a force from the sun. During the interval 1-2-3 the sun is pulling and changing the motion in various directions towards itself. To get a good approximation we will take the central position, or average position, at 2, and say that the whole effect during the interval 1-3 was to change the motion by some amount in the direction of the line 2-S. (Figure 3).
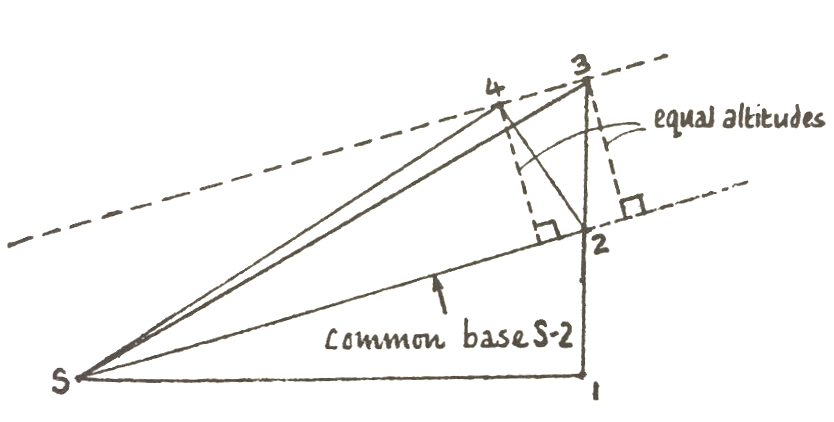
This means that though the particles were moving on the line 1-2, and would, were there no force, have continued to move on the same line in the next second, because of the influence of the sun the motion is altered by an amount that is poking in a direction parallel to the line 2-S. The next motion is therefore a compound of what the planet wanted to do and the change that has been induced by the action of the sun. So the planet does not really end up at position 3, but rather at position 4. Now we would like to compare the areas of the triangles 23S and 24S, and I will show you that those are equal. They have the same base, S-2. Do they have the same altitude? Sure, because they are included between parallel lines. The distance from 4 to the line S-2 is equal to the distance from 3 to line S-2 (extended). Thus the area of the triangle S24 is the same as S23. I proved earlier that S12 and S23 were equal in area, so we now know S12 = S24. So, in the actual orbital motion of the planet the areas swept out in the first second and the second second are equal. Therefore, by reasoning, we can see a connection between the fact that the force is towards the sun, and the fact that the areas are equal. Isn’t that ingenious? I borrowed it straight from Newton. It comes right out of the Principia, diagram and all. Only the letters are different, because he wrote in Latin and these are Arabic numerals…
Mathematics, then, is a way of going from one set of statements to another. It is evidently useful in physics, because we have these different ways in which we can speak of things, and mathematics permits us to develop consequences, to analyze the situations, and to change the laws in different ways to connect the various statements. In fact the total amount that a physicist knows is very little. He has only to remember the rules to get him from one place to another and he is all right, because all the various statements about equal times, the force being in the direction of the radius, and so on, are all interconnected by reasoning.
Chapter 2

